PART EIGHT

TAPERED BEAMS

 Most aircraft structural components are tapered to improve structural efficiency. All the analysis
done so far assumes the beams have uniform cross sections.

The effect of taper on direct stresses produces by bending moments are minimal if taper is small
and the sectional properties are determined at the section analysed.

However the effect of taper on shear stresses is considerable.

SINGLE WEB BEAM

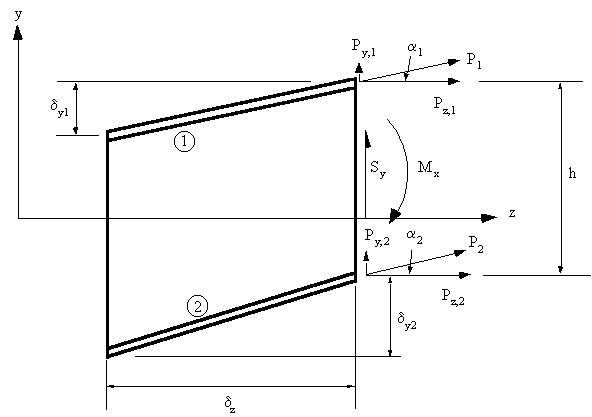
 Consider an idealised section of beam of length dz in the x-y plane with 2 flanges and a web.
At the RHS, it is subjected to a positive Moment Mx and Shear force Sy. The horizontal resultant
forces carried by the booms due to the bending moment Mx are: Pz,1 and Pz,2, and are defined by
the equation:

Where

            Bz = idealised boom area

The FBD of the beam section is:

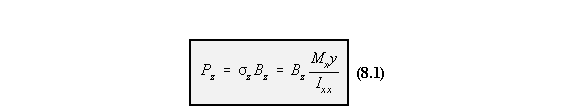
Figure 96: Effect of taper on single web beam analysis

From observation, the vertical components of the axial forces carried by the booms are:

Note :        The values for dy could be either negative or positive.

And from trigonometry, we can get that:

Which can then be used to determine the effect of taper on the stresses in the booms.

Now, the internal shear force Sy is equal to the shear force carried by the web Sy,w + the shear
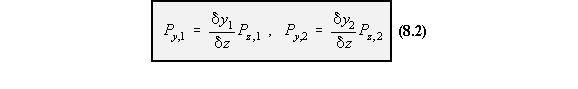
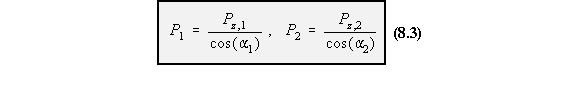
forces carried by the booms, Py,1 and Py,2. Thus:

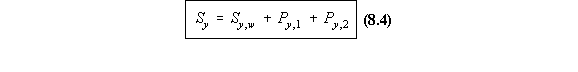
Since we are interested in determining the shear force carried by the web, then by substituting
equation (8.1) into (8.4) gives:

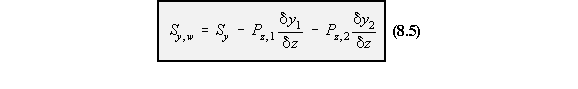
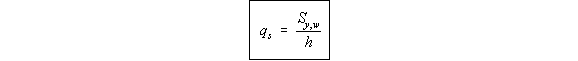
For an idealised web, the shear flow is then given by :

OPEN AND CLOSED BEAM SECTIONS

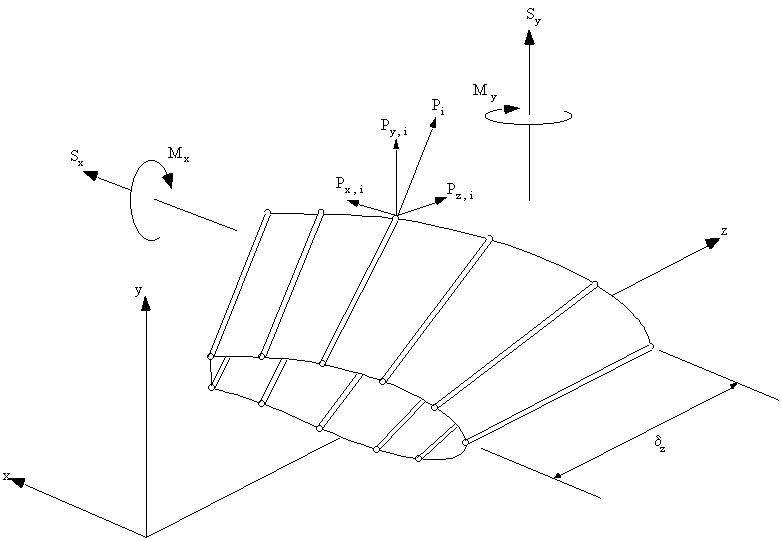
 The effect of taper on open and closed beam section is exactly the same, and is defined by the
analysis which follows.

Consider an idealised beam of length dz carrying positive shear loads Sy and Sx at the section z.
The beam is also subjected to bending moments Mx and My which produce a direct stress sz in
the booms.

Note :      The skin is only effective in shear.

The FBD for this boom is:

Figure 97: Effect of taper on the analysis of open or closed beam section
In boom i, the direct stress in z direction is: sz,i, and the component of axial force due to this
stress in the z direction is:

where Bi is area of ith boom

Look at the ith boom along the y-z and x-y axes gives:

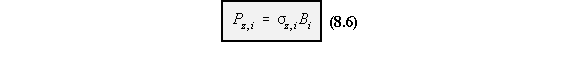
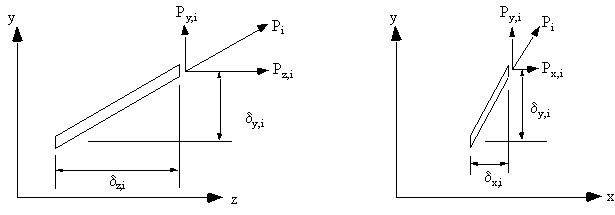
Figure 98: Effect of taper on ith beam of wing section
From these figures the relationships between Pyi, Pxi, & Pzi can be derived:

where:

Using these equations the true axial load in beam 'i' is:

or in terms of axial stress in z direction and taper is :

This equation give the effect of taper on the axial stress carried by the boom when this force is
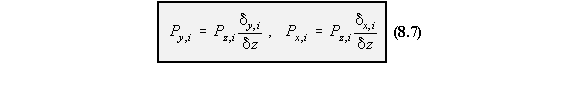
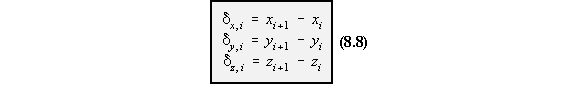
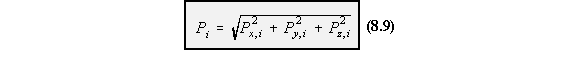
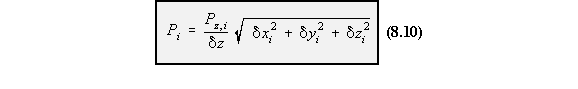
divided by the boom's true cross sectional area.

The shear loads Sy and Sx are reacted by the boom loads Px,i and Py,i and the shear flows in the
skin and web panels, such that:

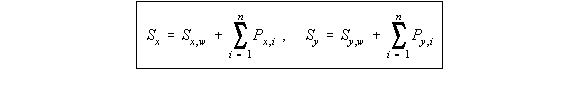
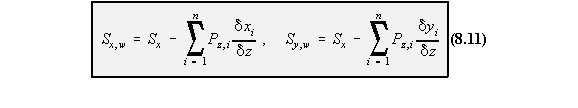
Substituting equation (8.7) into this and re-arranging it gives that:

The shear flow distribution in either open or closed beam sections are found as before, except
that instead of using Sy and Sx as the shear force terms you now use Sx,w and Sy,w. Which is the
fraction of the applied shear force carried by all skin and web panels.

Warning:      When taking moments to determine shear centre or qs,0 you must also consider
                     the moments generated by all the Px,i and Py,i which are the fractions of the
                     applied shear forces carried by the booms, equation (8.12).

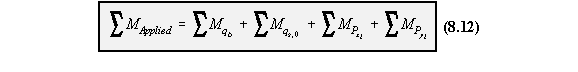
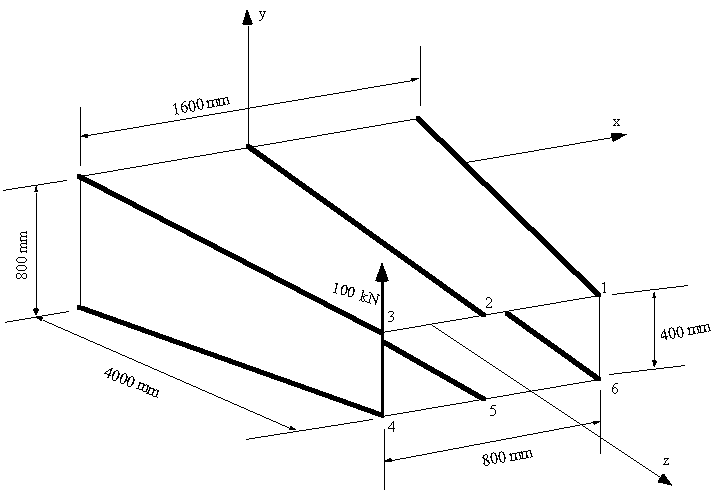
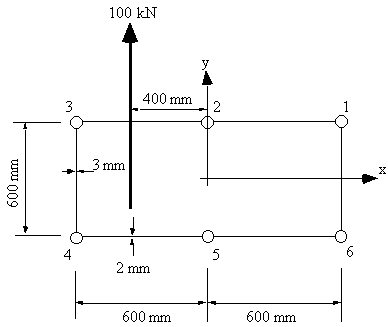
Example 13: An idealised cantilever beam is uniformly tapered along its length in the x and
                      y axis and carries a load of 100 kN at its free end. What are the boom forces
                     and the shear flow distribution in the walls at a section 2 m from the built in end.
                     The boom areas are B1 = B3 = B4 = B6 = 900 mm2, B2 = B5 = 1200 mm2.

Figure 99: Tapered box beam

The view of the cross section 2 m from the end is:

Figure 100: View of section 2 m from end
At 2 m from the end Sy = 100 kN, Sx = 0, My = 0 , Mx = -200kNm.

a)     Sectional Properties

b)     Determine Shear force carried by skin

Because of symmetry, Ixy = 0, so the direct stress equation becomes:

Equation for direct force is:

The best way to solve this problem is to create a table with all the necessary values.

From this table we can then obtain the resultant shear load carried by the skin, so using equations
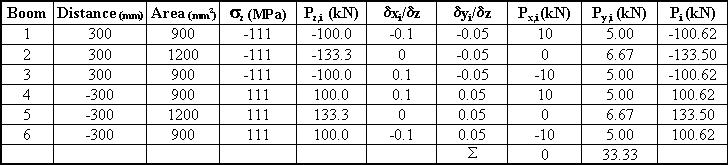
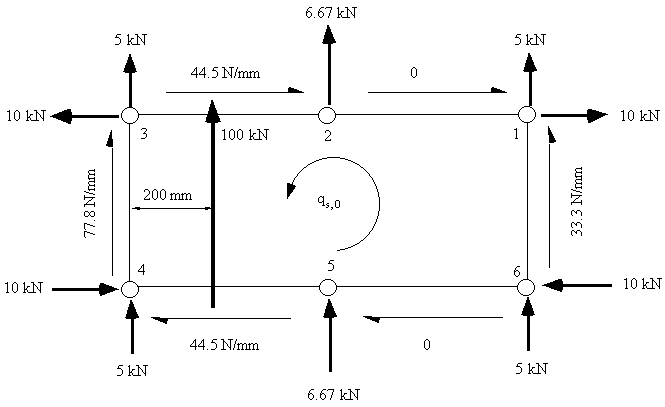
(8.10) we get that: Syw = 100 - 33.33 = 66.67 kN, and Sxw = 0 - 0 = 0 kN

c)     Determine Open Beam Shear Flow by cutting between booms 1 and 2

Because of symmetry, equation (6.12) simplifies to

Substituting for Shear flow and sectional properties gives:

Applying this equation together with equation (6.13) in a counterclockwise sense, starting with
boom 2 gives:

The section now looks like this:

Figure 102: Diagram of open beam shear flows, shear forces carried by booms because of taper and qs,0

d)     Determine qs,0 and closed beam shear flow

To do this take moments at any point, in this case moments were taken about the line of web
34.

100x103 x 200   =     10000x300 - 44.447x600x300 + 6666.7x600 + 5000x1200 - 10000x300
                                  + 33.335x600x1200 - 10000x300 + 5000x1200 + 6666.7x600 -
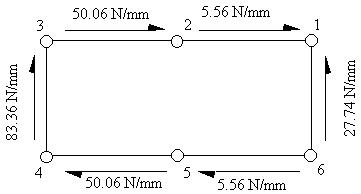
                                  44.447x600x300 + 10000x300 + 2x1200x600xqs,0

giving that qs,0 = - 5.56 N/mm, and so, the shear flow distribution is

Figure 103: Final shear flow distribution in tapered beam at 2 m from fixed end


...Back to Top