Area moment of inertia:
The area moment of inertia is the second moment of area around a given axis. For example, given the axis a-a and the shaded area shown, one calculates the second moment of the area by adding together l2dA for all the elements of area dA in the shaded area.
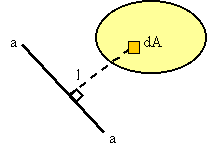
The area moment of inertia, denoted by I, can, therefore, be calculated from:
![]()
Formula for resultant moment of load about x-axis leads to the integral of y2dA over A. This integral is called the second moment of area A about the x-axis, or the moment of inertia of area A about the x-axis. It is usually denoted by Ix. So, in general, if we have a rectangular coordinate system as shown, one can define the area moment of inertia around the x and y axes by
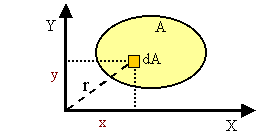
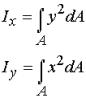
The polar area moment of inertia, denoted by JO, is the area moment of inertia about the z-axis given by
![]()
Note that since r2= x2+y2, one has the relation
JO=Ix+Iy
Radius of gyration:
The radius of gyration is the distance k away from the axis that all the area can be concentrated to result in the same moment of inertia. That is,
I = k2A
For a given area, one can define the radius of gyration around the x-axis, denoted by kx, the radius of gyration around the y-axis, denoted by ky, and the radius of gyration around the z-axis, denoted by kO. These are calculated from the relations
![]()
It can easily to show from JO=Ix+Iy that
![]()
Parallel axis theorem:
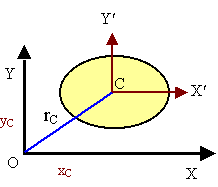
The parallel axis theorem is a relation between the moment of inertia about an axis passing through the centroid and the moment of inertia about any parallel axis.
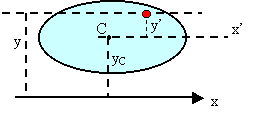
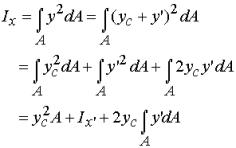
Since 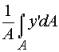 gives the distance of the centroid above the x'-axis,
and since the this distance is zero, one must conclude that the integral in the last term
is zero so that the parallel axis theorem states that
gives the distance of the centroid above the x'-axis,
and since the this distance is zero, one must conclude that the integral in the last term
is zero so that the parallel axis theorem states that
![]()
where x' must pass through the centroid of the area. In this same way, one can show that
![]()
 In
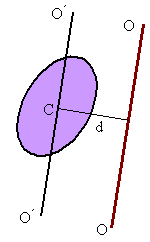
general, one can use the parallel axis theorem for any two parallel axes as long as one
passes through the centroid. As shown in the picture, this is written as
In
general, one can use the parallel axis theorem for any two parallel axes as long as one
passes through the centroid. As shown in the picture, this is written as ![]() ,
,
where ![]() is the moment of inertia about the axis O'-O'
passing through the centroid, I is the moment of inertia about the axis O-O, and d
is the perpendicular distance between the two parallel axis.
is the moment of inertia about the axis O'-O'
passing through the centroid, I is the moment of inertia about the axis O-O, and d
is the perpendicular distance between the two parallel axis.
The moment of inertia of composite bodies can be calculated by adding together the moment of inertial of each of its sections. The only thing to remember is that all moments of inertia must be evaluated bout the same axis. Therefore, for example,
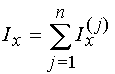
To calculate the area moment of inertia of the composite body
constructed of the three segments shown, one evaluates the moment of inertial of each part
about the x-axis and adds the three together.

